단단한 강화학습 코드 정리, chap12

ShangtongZhang github

단단한 강화학습 책의 코드를 공부하기 위해 쓰여진 글이다.

random_walk

# all states
N_STATES = 19

# all states but terminal states
STATES = np.arange(1, N_STATES + 1)

# start from the middle state
START_STATE = 10

# two terminal states
# an action leading to the left terminal state has reward -1
# an action leading to the right terminal state has reward 1
END_STATES = [0, N_STATES + 1]

# true state values from Bellman equation
TRUE_VALUE = np.arange(-20, 22, 2) / 20.0
TRUE_VALUE[0] = TRUE_VALUE[N_STATES + 1] = 0.0

• (1~2) : SuttonCode_ch07와 같이 19개의 상태를 갖는다.
• (4~5) : terminal state를 제외한 상태 배열 $[1, 19]$
• (7~8) : 시작 상태를 10으로 하여 terminal state를 제외하고 좌우로 9개의 상태를 가진다.
• (10~13) : terminal state를 0, N_STATES+1 (=20)로 한다. 가장 왼쪽(=0)은 -1, 가장 오른쪽(=20)은 1의 보상을 얻는다.
• (15~17) : 실제값을 지정한다. $[-20, -18, …, 18, 20]$을 20으로 나눠 $[-1, -0.9, …, 0.9, 1.0]$를 만들고 terminal state의 인덱스인 0, 20을 0으로 바꾼다.

ValueFunction

# base class for lambda-based algorithms in this chapter
# In this example, we use the simplest linear feature function, state aggregation.
# And we use exact 19 groups, so the weights for each group is exact the value for that state
class ValueFunction:
    # @rate: lambda, as it's a keyword in python, so I call it rate
    # @stepSize: alpha, step size for update
    def __init__(self, rate, step_size):
        self.rate = rate
        self.step_size = step_size
        self.weights = np.zeros(N_STATES + 2)

    # the state value is just the weight
    def value(self, state):
        return self.weights[state]

    # feed the algorithm with new observation
    # derived class should override this function
    def learn(self, state, reward):
        return

    # initialize some variables at the beginning of each episode
    # must be called at the very beginning of each episode
    # derived class should override this function
    def new_episode(self):
        return

• (1~4) : $\lambda$ 기반 알고리즘의 base 클래스. 다른 알고리즘 클래스는 이 ValueFunction을 상속한다. 상태 결집을 사용하여 19개의 그룹을 나타내는데 19개의 값을 사용하므로 가중치는 그 상태의 값이 된다.
• (5~10) : lambda가 파이썬 키워드이므로 rate로 바꾼다. $\lambda$, $\alpha$를 클래스 내부에 저장하고 terminal state를 포함한 19+2개의 가치를 나타내는 배열을 0으로 초기화한다
• (12~14) : 상태의 가치는 가중치를 그대로 반환한다.
• (16~19) : 상태와 보상으로 학습한다. 파생 클래스는 이 함수를 오버라이딩해야한다.
• (21~25) : 에피소드 시작시에 호출되어야 하며 몇몇 변수가 초기화된다. 파생클래스는 이 함수를 오버라이딩해야한다.

OffLineLambdaReturn

# Off-line lambda-return algorithm
class OffLineLambdaReturn(ValueFunction):
    def __init__(self, rate, step_size):
        ValueFunction.__init__(self, rate, step_size)
        # To accelerate learning, set a truncate value for power of lambda
        self.rate_truncate = 1e-3

    def new_episode(self):
        # initialize the trajectory
        self.trajectory = [START_STATE]
        # only need to track the last reward in one episode, as all others are 0
        self.reward = 0.0

    def learn(self, state, reward):
        # add the new state to the trajectory
        self.trajectory.append(state)
        if state in END_STATES:
            # start off-line learning once the episode ends
            self.reward = reward
            self.T = len(self.trajectory) - 1
            self.off_line_learn()

    # get the n-step return from the given time
    def n_step_return_from_time(self, n, time):
        # gamma is always 1 and rewards are zero except for the last reward
        # the formula can be simplified
        end_time = min(time + n, self.T)
        returns = self.value(self.trajectory[end_time])
        if end_time == self.T:
            returns += self.reward
        return returns

    # get the lambda-return from the given time
    def lambda_return_from_time(self, time):
        returns = 0.0
        lambda_power = 1
        for n in range(1, self.T - time):
            returns += lambda_power * self.n_step_return_from_time(n, time)
            lambda_power *= self.rate
            if lambda_power < self.rate_truncate:
                # If the power of lambda has been too small, discard all the following sequences
                break
        returns *= 1 - self.rate
        if lambda_power >= self.rate_truncate:
            returns += lambda_power * self.reward
        return returns

    # perform off-line learning at the end of an episode
    def off_line_learn(self):
        for time in range(self.T):
            # update for each state in the trajectory
            state = self.trajectory[time]
            delta = self.lambda_return_from_time(time) - self.value(state)
            delta *= self.step_size
            self.weights[state] += delta

• (1~2) : Offline lambda return 알고리즘을 구현한 클래스이며 ValueFunction을 상속한다.
• (3~4) : 상속한 ValueFunction의 생성자를 호출하여 rate($\lambda$), step_size($\alpha$), weights 배열을 클래스 변수로 저장한다.
• (5~6) : 학습을 더 빠르게 하기 위해 $\lambda$의 제곱이 0.001보다 작으면 무시한다.
• (8) : 에피소드 시작시에 호출되는 함수
• (9~10) : 에피소드의 궤적을 저장하는 self.trajectory에 START_STATE를 넣고 시작한다.
• (11~12) : terminal state를 제외하고 보상이 0이므로 마지막 상태의 보상만 추적한다
• (14) : 학습을 위한 함수로 state와 reward를 인수로 받는다.
• (15~16) : trajectory에 state를 추가한다.
• (17~21) : state가 terminal state일 경우 (에피소드가 끝날 경우), 클래스 변수에 reward, 에피소드의 길이(self.T)를 저장하고 self.off_line_learn을 호출한다.
• (23~24) : $n$, $t$를 통해 $G_{t:t+n}$, (=n-step return)을 구하는 함수이다.
• (25~26) : $\gamma$가 1이고 마지막 보상을 제외하고 보상은 0이므로 공식이 단순화될 수 있다.

\[G_{t:t+n} \doteq R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1}R_{t+n} + \gamma^{n} V_{t+n-1}(S_{t+n})\]

• (27) : $t+n$과 $T$중 더 빠른 것을 end_time에 저장한다. 여기서 end_time은 terminal_state가 될 수 없다. 왜냐하면 end_time이 취할 수 있는 최대값이 self.T인데 self.T=len(self.trajectory) - 1이기 때문에 trajectory에 마지막으로 추가되는 terminal state가 제외된다.
• (28) : returns에 $\gamma^{n}V_{t+n-1}(S_{t+n})$을 저장하는데 $\gamma=1$ 이므로 $V_{t+n-1}(S_{t+n})$을 대입한다.
• (29~30) : end_time == self.T이면 returns에 self.reward를 더한다. 자세히 말해보자면 end_state=min(time + n, self.T)이기 때문에 end_time == self.T라는 것은 $\left [ t, t+n\right ]$ 안에 $T-1$가 포함되어 terminal state로 가는 과정에서 1또는 -1의 보상을 받았다는 뜻이다. 그렇기 때문에 에피소드 종료시에 self.reward에 저장했던 보상값을 더한다.
• (31) : 누적된 보상값($G_{t:t+n}$)을 반환한다.
• (33~34) : $t$에 해당하는 $G^{\lambda}_{t}$를 구하는 함수이다.
• (35) : 보샹을 누적할 returns 변수를 0으로 초기화한다.
• (36) : $\lambda$를 누적제곱할 항이다. 처음에는 1이고 계속해서 $\lambda$를 곱한다.
• (37) : $\sum^{T-t-1}_{n=1}$를 의미하는 반복문이다
• (38) : 누적하여 합하여 $\sum$의 효과를 낸다. $\sum_{n=1}^{T-t-1}\lambda^{n-1}G_{t:t+n}$을 의미한다. $G_{t:t+n}$은 self.n_step_return_from_time를 통해 얻는다.
• (39) : 반복마다 lambda_power에 $\lambda$를 곱함으로써 $\lambda^{n-1}$의 기능을 한다.
• (40~42) : (5~6) 과 같이 $\lambda^{n-1}$이 self.rate_truncate=1e3 보다 작으면 이후 과정을 버린다.
• (43) : $(1-\lambda)\sum_{n=1}^{T-t-1}\lambda^{n-1}G_{t:t+n}$ 를 계산한다
• (44~45) : $\lambda^{n-1}$이 계속 진행되었다면 $\lambda^{T-t-2}$ 까지 진행되었을 것이고 거기에 $\lambda$를 곱하면 $\lambda^{T-t-1}$이 될 것이다. 코드상에서는 반복문에서 첫 값을 사용하고 (39) 처럼 그 후에 곱하고 다음에 사용하기 때문에 곱해진 해당 값을 구대로 사용하면 된다. 이는 $(12.3)$에서 $\lambda^{T-t-1}G_t$를 의미한다. 해당 구현상에서는 $\lambda^{T-t-1}$이 self.rate_truncate보다 작으면 무시한다.
• (46) :

\[G_t^{\lambda}=(1-\lambda)\sum_{n=1}^{T-t-1}\lambda^{n-1}G_{t:t+n} + \lambda^{T-t-1}G_t\]

• (48~49) : 에피소드 종료시에 offline learning을 수행한다.
• (50) : 에피소드의 길이만큼 반복한다. 에피소드의 길이는 terminal state를 제외하고 거쳐간 모든 상태들의 개수이다
• (51) : trajectory의 각각의 상태들을 갱신한다.
• (52) : 업데이트하게 될 해당 시간의 상태를 저장한다. $S_t$를 의미한다.
• (53) : $G^{\lambda}_{t} - \hat{v}(S_t, \textbf{w})$를 의미하며 $G^{\lambda}_{t}$는 self.lambda_return_from_time를 통해 얻는다.

TemporalDifferenceLambda

# TD(lambda) algorithm
class TemporalDifferenceLambda(ValueFunction):
    def __init__(self, rate, step_size):
        ValueFunction.__init__(self, rate, step_size)
        self.new_episode()

    def new_episode(self):
        # initialize the eligibility trace
        self.eligibility = np.zeros(N_STATES + 2)
        # initialize the beginning state
        self.last_state = START_STATE

    def learn(self, state, reward):
        # update the eligibility trace and weights
        self.eligibility *= self.rate
        self.eligibility[self.last_state] += 1
        delta = reward + self.value(state) - self.value(self.last_state)
        delta *= self.step_size
        self.weights += delta * self.eligibility
        self.last_state = state

• (1~2) : $\text{TD}(\lambda)$를 나타내는 클래스, ValueFunction을 상속한다.
• (3~4) : 상속한 ValueFunction의 생성자를 호출하여 weights 배열, rate($\lambda$), step_size($\alpha$) 을 클래스 변수로 저장한다.
• (5) : 각 에피소드별로 random_walk 호출시에 new_episode()가 실행되므로 중복된 코드이다.
• (7) : 새로운 에피소드가 시작될때 호출되는 함수이다.
• (8~9) : 적격 흔적 벡터를 0으로 초기화한다.
• (10~11) : 마지막(최근) 상태를 시작상태로 초기화한다.
• (13) : 상태와 보상을 인수로 받는 클래스 함수이다. 여기서 $\nabla\hat{v}(S, \textbf{w})=1$, $\gamma = 1$ 이다.
• (15~16) : $\textbf{z} \leftarrow \gamma \lambda \textbf{z} + \nabla\hat{v}(S, \textbf{w})$
  • eligibility : $\textbf{z}$
  • rate : $\lambda$
• (17) : $\delta \leftarrow R + \gamma \hat{v}(S’, \textbf{w})-\hat{v}(S, \textbf{w})$
  • delta : $\delta$
  • reward : $R$
• (18~19) : $\textbf{w} \leftarrow \textbf{w} + \alpha \delta \textbf{z}$
  • step_size : $\alpha$
• (20) : $S \leftarrow S’$

TrueOnlineTemporalDifferenceLambda

# True online TD(lambda) algorithm
class TrueOnlineTemporalDifferenceLambda(ValueFunction):
    def __init__(self, rate, step_size):
        ValueFunction.__init__(self, rate, step_size)

    def new_episode(self):
        # initialize the eligibility trace
        self.eligibility = np.zeros(N_STATES + 2)
        # initialize the beginning state
        self.last_state = START_STATE
        # initialize the old state value
        self.old_state_value = 0.0

    def learn(self, state, reward):
        # update the eligibility trace and weights
        last_state_value = self.value(self.last_state)
        state_value = self.value(state)
        dutch = 1 - self.step_size * self.rate * self.eligibility[self.last_state]
        self.eligibility *= self.rate
        self.eligibility[self.last_state] += dutch
        delta = reward + state_value - last_state_value
        self.weights += self.step_size * (delta + last_state_value - self.old_state_value) * self.eligibility
        self.weights[self.last_state] -= self.step_size * (last_state_value - self.old_state_value)
        self.old_state_value = state_value
        self.last_state = state

• (1~2) : $\text{TD}(\lambda)$를 나타내는 클래스, ValueFunction을 상속한다.
• (3~4) : 상속한 ValueFunction의 생성자를 호출하여 weights 배열, rate($\lambda$), step_size($\alpha$) 을 클래스 변수로 저장한다.
• (6) : 새로운 에피소드가 시작될때 호출되는 함수이다.
• (7~8) : 적격 흔적 벡터($\textbf{z}$)를 0으로 초기화한다.
• (9~10) : 마지막(최근) 상태를 시작상태로 초기화한다.
• (11~12) : 이전 상태 가치($V_{\text{old}}$)를 0으로 초기화한다
• (14) : 상태($S=\textbf{x}$)와 보상($R$)을 인수로 받아 가중치를 갱신하는 함수, $\gamma=1$
• (16) : $V \leftarrow \textbf{w}^{\top}\textbf{x}$
  • last_state_value : $V$
• (17) : $V’ \leftarrow \textbf{w}^{\top}\textbf{x}’$
  • state_value : $V’$
• (18) : $\text{dutch} \leftarrow (1-\alpha \gamma \lambda \textbf{z}^{\top}_{t-1} \textbf{x})\textbf{x}$
  • $\textbf{x}_t \doteq \textbf{x}(S_t)$인데 여기서는 근사하지 않고 표에서 그 상태 자체로 계산하므로 one-hot 벡터이다. 즉 벡터로 보면 벡터로 봐도 되고 단일 스칼라 값으로 계산해도 구현상 문제없다는 뜻이다.
  • step_size : $\alpha$
  • rate : $\lambda$
  • eligibility : $\textbf{z}$
• (19~20) : $\textbf{z} \leftarrow \gamma \lambda \textbf{z} + (1-\alpha \gamma \lambda \textbf{z}^{\top}_{t-1} \textbf{x})\textbf{x}$
• (21) : $\delta \leftarrow R + \gamma \hat{v}(S’, \textbf{w})-\hat{v}(S, \textbf{w})$
  • delta : $\delta$
• (22~23) : $\textbf{w} \leftarrow \textbf{w} + \alpha(\delta+V-V_{\text{old}})\textbf{z} - \alpha(V-V_{\text{old}})\textbf{x}$
• (24) : $V_{\text{old}} \leftarrow V’$
• (25) : $\textbf{x} \leftarrow \textbf{x}’$

parameter_sweep

# general plot framework
# @valueFunctionGenerator: generate an instance of value function
# @runs: specify the number of independent runs
# @lambdas: a series of different lambda values
# @alphas: sequences of step size for each lambda
def parameter_sweep(value_function_generator, runs, lambdas, alphas):
    # play for 10 episodes for each run
    episodes = 10
    # track the rms errors
    errors = [np.zeros(len(alphas_)) for alphas_ in alphas]
    for run in tqdm(range(runs)):
        for lambdaIndex, rate in enumerate(lambdas):
            for alphaIndex, alpha in enumerate(alphas[lambdaIndex]):
                valueFunction = value_function_generator(rate, alpha)
                for episode in range(episodes):
                    random_walk(valueFunction)
                    stateValues = [valueFunction.value(state) for state in STATES]
                    errors[lambdaIndex][alphaIndex] += np.sqrt(np.mean(np.power(stateValues - TRUE_VALUE[1: -1], 2)))

    # average over runs and episodes
    for error in errors:
        error /= episodes * runs

    for i in range(len(lambdas)):
        plt.plot(alphas[i], errors[i], label='lambda = ' + str(lambdas[i]))
    plt.xlabel('alpha')
    plt.ylabel('RMS error')
    plt.legend()

• (1~6) :
  • value_function_generator : value function의 객체를 생성한다(클래스를 넣는다)
  • runs : 독립적인 실행의 횟수
  • lambdas : 서로 다른 lambda 값 배열
  • alphas : 각 lambdas에 해당하는 step size 배열
• (7~8) : 각 독립적인 실행은 10번의 에피소드를 진행한다.
• (9~10) : RMS error를 저장하는 행렬, i행 j열이면 i번째 $\lambda$를 적용했을 때 대응하는 alphas의 i번째 행의 j열의 $\alpha$ 값의 RMS error이다.
• (11) : runs 횟수만큼 독립 실행이 일어난다
• (12~13) : $\lambda$ 값을 결정하면 그에 해당하는 배열을 alphas 배열에서 alphas[lambdaIndex]를 통해 얻은 후 배열의 각 $\alpha$ 값에 대해 실험을 진행한다.
• (14) : value_function_generator에 $\lambda, \alpha$를 파라미터로 넣은 객체를 valueFunction에 저장한다.

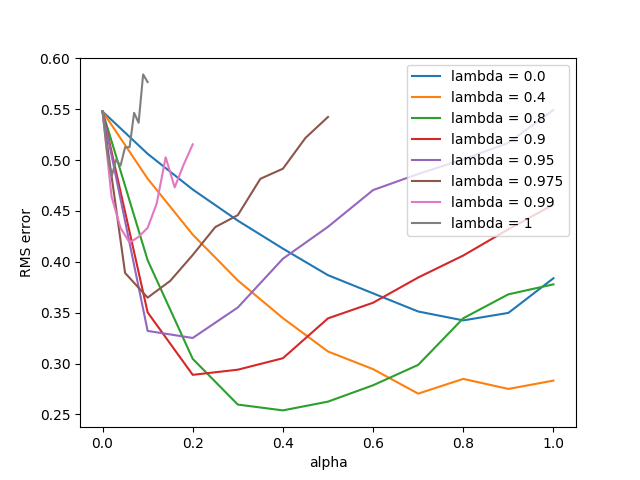
figure 12_3

# Figure 12.3: Off-line lambda-return algorithm
def figure_12_3():
    lambdas = [0.0, 0.4, 0.8, 0.9, 0.95, 0.975, 0.99, 1]
    alphas = [np.arange(0, 1.1, 0.1),
              np.arange(0, 1.1, 0.1),
              np.arange(0, 1.1, 0.1),
              np.arange(0, 1.1, 0.1),
              np.arange(0, 1.1, 0.1),
              np.arange(0, 0.55, 0.05),
              np.arange(0, 0.22, 0.02),
              np.arange(0, 0.11, 0.01)]
    parameter_sweep(OffLineLambdaReturn, 50, lambdas, alphas)

• (3) : 실험에 사용할 $\lambda$ 값의 목록이다.
• (4~11) : 같은 인덱스의 $\lambda$에 대응하는 $\alpha$의 값의 목록

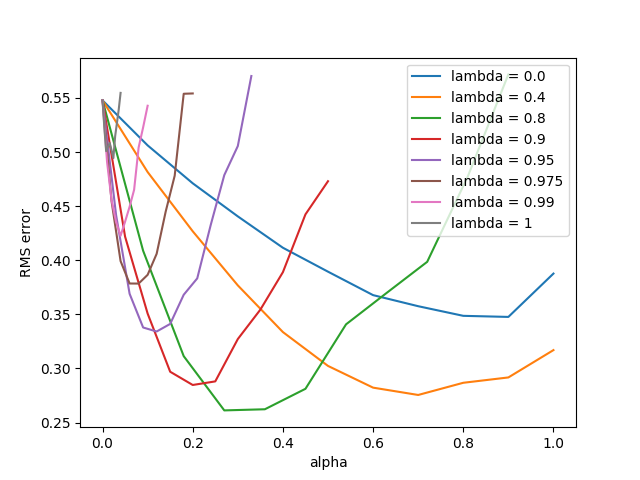
figure 12_6

# Figure 12.6: TD(lambda) algorithm
def figure_12_6():
    lambdas = [0.0, 0.4, 0.8, 0.9, 0.95, 0.975, 0.99, 1]
    alphas = [np.arange(0, 1.1, 0.1),
              np.arange(0, 1.1, 0.1),
              np.arange(0, 0.99, 0.09),
              np.arange(0, 0.55, 0.05),
              np.arange(0, 0.33, 0.03),
              np.arange(0, 0.22, 0.02),
              np.arange(0, 0.11, 0.01),
              np.arange(0, 0.044, 0.004)]
    parameter_sweep(TemporalDifferenceLambda, 50, lambdas, alphas)

• (3) : 실험에 사용할 $\lambda$ 값의 목록이다.
• (4~11) : 같은 인덱스의 $\lambda$에 대응하는 $\alpha$의 값의 목록

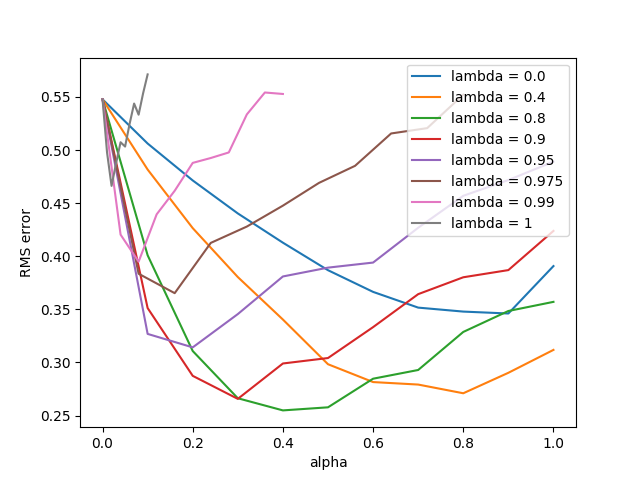
figure 12_8

# Figure 12.7: True online TD(lambda) algorithm
def figure_12_8():
    lambdas = [0.0, 0.4, 0.8, 0.9, 0.95, 0.975, 0.99, 1]
    alphas = [np.arange(0, 1.1, 0.1),
              np.arange(0, 1.1, 0.1),
              np.arange(0, 1.1, 0.1),
              np.arange(0, 1.1, 0.1),
              np.arange(0, 1.1, 0.1),
              np.arange(0, 0.88, 0.08),
              np.arange(0, 0.44, 0.04),
              np.arange(0, 0.11, 0.01)]
    parameter_sweep(TrueOnlineTemporalDifferenceLambda, 50, lambdas, alphas)

• (3) : 실험에 사용할 $\lambda$ 값의 목록이다.
• (4~11) : 같은 인덱스의 $\lambda$에 대응하는 $\alpha$의 값의 목록