단단한 강화학습 코드 정리, chap4

2022-10-03

단단한 강화학습 책의 코드를 공부하기 위해 쓰여진 글이다.

// TODO : 포아송분포 공부 후 figure4.2 보충

`figure 4.2`

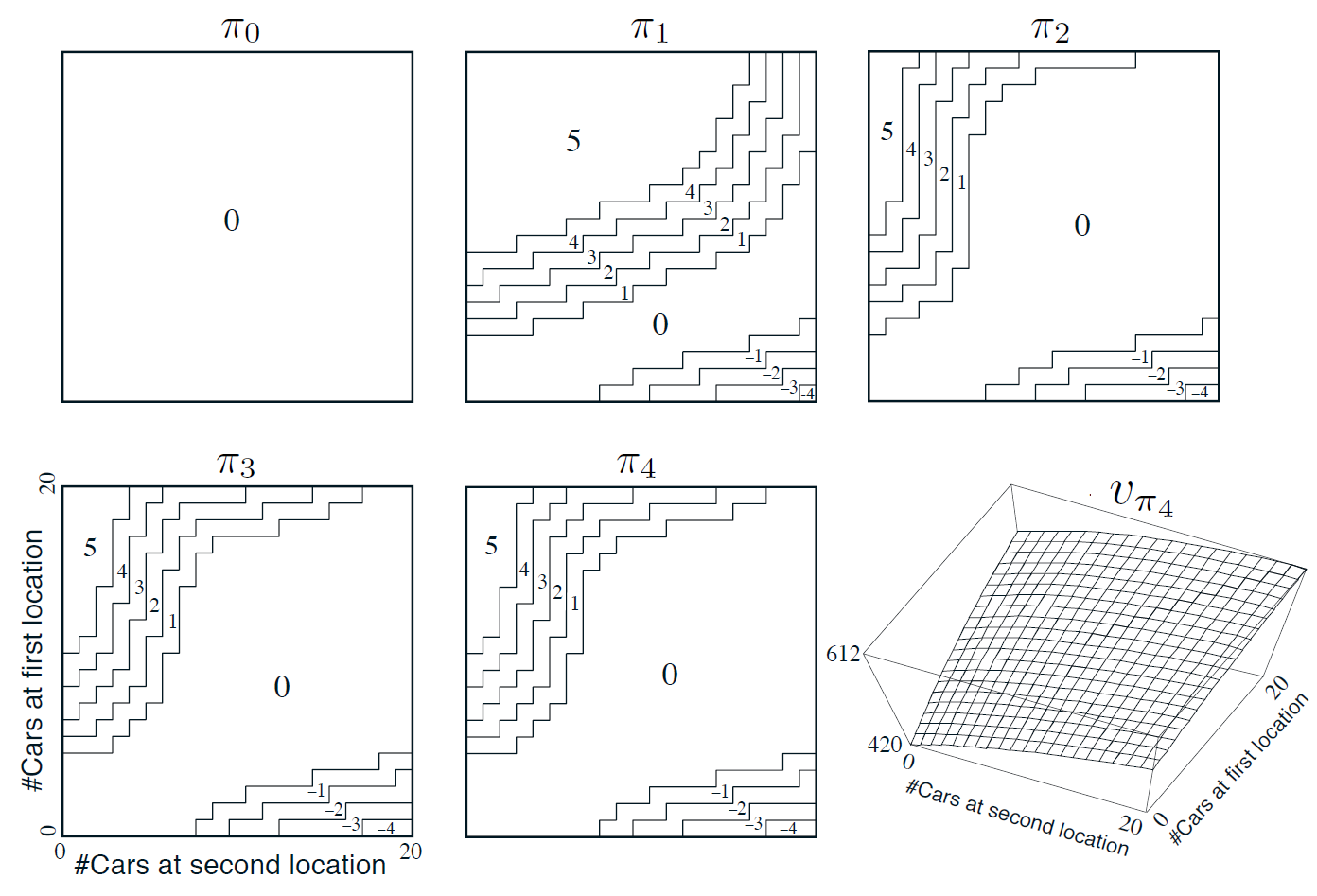
figure_4_2

자동차 렌탈

매일 몇 명의 고객이 자동차를 렌트하기 위해 각 지점을 방문한다. 차를 빌려주면 10달러의 보상을 받고, 빌려줄 차가 없으면 거래가 무산된다. 차는 회수된 다음 날부터 다시 대여가 가능하다. 두 지점에 있는 차량을 한 대당 2달러의 비용을 들여 교환할 수 있다. 한 지점에서 대여되고 회수되는 자동차의 개수가 Poisson Distribution을 따르는 확률변수라고 가정한다. Poisson Distribution을 따른다는 것은 자동차의 개수가 $n$이 될 확률이 $\frac{\lambda^n}{n!}e^{-\lambda}$임을 의미한다. 이때 $\lambda$는 개수의 평균값을 나타낸다. 대여되는 자동차 개수에 대한 $\lambda$의 값이 첫번째와 두 번째 지점에서 각각 $3$과 $4$이고, 회수되는 자동차 개수에 대한 $\lambda$ 값은 각각 $3$과 $2$라고 하자. 각 지점은 최대 20대까지만 자동차를 보유할 수 있다(20대 초과시 본사로 회수). 하루 밤사이 두 지점 사이에서 교환할 수 있는 자동차의 최대 개수는 5대. 할인률을 $\lambda$로 하고 이 문제를 연속적인 MDP 문제로 형식화한다.

시간 단계 : 하루 단위이고
상태 : 하루가 끝나는 시점에 각 지점이 보유한 자동차의 개수
행동 : 밤사이 두 지점 사이에서 교환되는 자동차의 총 개수

figure 4.2는 차량을 교환하지 않는 정책을 시작으로 하여 정책 반복을 수행한 결과를 보여준다. 처음 다섯 개의 다이어그램은 각 지점이 하루의 마지막 시점에 보유한 자동차의 개수가 주어졌을 때, 첫 번째 지점에서 두 번째 지점으로 옮겨져야 할 자동차의 개수가 얼마인지 보여준다.(음의 값: 두번째->첫 번째) 각 정책에 이웃한 다음 정책은 바로 이전 정책보다 분명히 향상되며, 마지막 정책이 최적 정책이다.

`Car Rental`

matplotlib.use('Agg')
# maximum # of cars in each location
MAX_CARS = 20
# maximum # of cars to move during night
MAX_MOVE_OF_CARS = 5
# expectation for rental requests in first location
RENTAL_REQUEST_FIRST_LOC = 3
# expectation for rental requests in second location
RENTAL_REQUEST_SECOND_LOC = 4
# expectation for # of cars returned in first location
RETURNS_FIRST_LOC = 3
# expectation for # of cars returned in second location
RETURNS_SECOND_LOC = 2
DISCOUNT = 0.9
# credit earned by a car
RENTAL_CREDIT = 10
# cost of moving a car
MOVE_CAR_COST = 2
# all possible actions
actions = np.arange(-MAX_MOVE_OF_CARS, MAX_MOVE_OF_CARS + 1)
# An up bound for poisson distribution
# If n is greater than this value, then the probability of getting n is truncated to 0
POISSON_UPPER_BOUND = 11

(3) : MAX_CARS=20 : 각 지점이 보유할 수 있는 자동차의 최대값
(5) : MAX_MOVE_OF_CARS : 하루 밤사이 두 지점 사이에서 교환할 수 있는 자동차의 최대 개수
(7) : RENTAL_REQUEST_FIRST_LOC = 3 : 첫 번째 지점에서 대여되는 자동차 개수에 대한 $\lambda$
(9) : RENTAL_REQUEST_SECOND_LOC = 4 : 두 번째 지점에서 대여되는 자동차 개수에 대한 $\lambda$
(11) : RETURNS_FIRST_LOC = 3 : 첫 번째 지점에서 회수되는 자동차 개수에 대한 $\lambda$
(13) : RETURNS_SECOND_LOC = 2 : 두 번째 지점에서 회수되는 자동차 개수에 대한 $\lambda$
(16) : RENTAL_CREDIT = 10 : 차를 빌려주고 본사로부터 받는 보상
(18) : MOVE_CAR_COST = 2 : 차량 교환에 드는 비용
(20) : action은 [-5,5]의 범위를 갖는다, 양수: 1->2, 음수: 2->1
(23) : POISSON_UPPER_BOUND = 11 n이 11보다 클 경우 확률은 0이 된다.

# Probability for poisson distribution
# @lam: lambda should be less than 10 for this function
poisson_cache = dict()

def poisson_probability(n, lam):
    global poisson_cache
    key = n * 10 + lam
    if key not in poisson_cache:
        poisson_cache[key] = poisson.pmf(n, lam)
    return poisson_cache[key]

푸아송 분포($\frac{\lambda^n}{n!}e^{-\lambda}$)를 구현하는 코드이다. 해당 $n$, $\lambda$에 대한 pmf를 반환한다.

(3) : poisson_probability 함수 호출마다 확률을 새로 구하는 것을 방지하기 위하여 한번 구했다면 그 값을 저장하는 dict()(=Hash Table)을 선언한다.
(7) : $\lambda < 10$이기 때문에 $n$에 10을 곱하면 이는 $\lambda$에 영향을 주지 못하며이는 유일한 key로 적용 가능하다.
(8~9) : key가 poisson_cache에 없을 경우 poisson.pmf(n, lam)($=\frac{\lambda^n}{n!}e^{-\lambda}$)을 계산하여 해당 key값에 저장한다.
(10) : poisson_cache[key]를 반환한다.

def expected_return(state, action, state_value, constant_returned_cars):
    """
    @state: [# of cars in first location, # of cars in second location]
    @action: positive if moving cars from first location to second location,
            negative if moving cars from second location to first location
    @stateValue: state value matrix
    @constant_returned_cars:  if set True, model is simplified such that
    the # of cars returned in daytime becomes constant
    rather than a random value from poisson distribution, which will reduce calculation time
    and leave the optimal policy/value state matrix almost the same
    """
    # initailize total return
    returns = 0.0

    # cost for moving cars
    returns -= MOVE_CAR_COST * abs(action)

    # moving cars
    NUM_OF_CARS_FIRST_LOC = min(state[0] - action, MAX_CARS)
    NUM_OF_CARS_SECOND_LOC = min(state[1] + action, MAX_CARS)

    # go through all possible rental requests
    for rental_request_first_loc in range(POISSON_UPPER_BOUND):
        for rental_request_second_loc in range(POISSON_UPPER_BOUND):
            # probability for current combination of rental requests
            prob = poisson_probability(rental_request_first_loc, RENTAL_REQUEST_FIRST_LOC) * \
                poisson_probability(rental_request_second_loc, RENTAL_REQUEST_SECOND_LOC)

            num_of_cars_first_loc = NUM_OF_CARS_FIRST_LOC
            num_of_cars_second_loc = NUM_OF_CARS_SECOND_LOC

            # valid rental requests should be less than actual # of cars
            valid_rental_first_loc = min(num_of_cars_first_loc, rental_request_first_loc)
            valid_rental_second_loc = min(num_of_cars_second_loc, rental_request_second_loc)

            # get credits for renting
            reward = (valid_rental_first_loc + valid_rental_second_loc) * RENTAL_CREDIT
            num_of_cars_first_loc -= valid_rental_first_loc
            num_of_cars_second_loc -= valid_rental_second_loc

            if constant_returned_cars:
                # get returned cars, those cars can be used for renting tomorrow
                returned_cars_first_loc = RETURNS_FIRST_LOC
                returned_cars_second_loc = RETURNS_SECOND_LOC
                num_of_cars_first_loc = min(num_of_cars_first_loc + returned_cars_first_loc, MAX_CARS)
                num_of_cars_second_loc = min(num_of_cars_second_loc + returned_cars_second_loc, MAX_CARS)
                returns += prob * (reward + DISCOUNT * state_value[num_of_cars_first_loc, num_of_cars_second_loc])
            else:
                for returned_cars_first_loc in range(POISSON_UPPER_BOUND):
                    for returned_cars_second_loc in range(POISSON_UPPER_BOUND):
                        prob_return = poisson_probability(
                            returned_cars_first_loc, RETURNS_FIRST_LOC) * poisson_probability(returned_cars_second_loc, RETURNS_SECOND_LOC)
                        num_of_cars_first_loc_ = min(num_of_cars_first_loc + returned_cars_first_loc, MAX_CARS)
                        num_of_cars_second_loc_ = min(num_of_cars_second_loc + returned_cars_second_loc, MAX_CARS)
                        prob_ = prob_return * prob
                        returns += prob_ * (reward + DISCOUNT *
                                            state_value[num_of_cars_first_loc_, num_of_cars_second_loc_])
    return returns

(3~10)
- state : [첫 번째 지점의 차 개수, 두 번째 지점의 차 개수]
- action : 양수 : 1->2, 음수 : 2->1
(13) : returns를 0으로 초기화한다.
(16) : action의 절댓값(=옮기는 차량 개수) * MOVE_CAR_COST(=2)를 returns에서 뺀다
(19~20) : NUM_OF_CARS_FIRST/SECOND_LOC : state에서 action을 반영한 자동차의 개수를 초기화한다, 최대 개수인 MAX_CARS(=20)을 넘을 경우 20으로 초기화된다.
(26~27) : // TODO
(29~30) : 상수 변수로 선언된 NUM_OF_CARS_(N)_LOC를 변형 가능한 num_of_cars_(n)_loc 변수로 옮긴다.
(33~34) : 렌탈 요청 개수를 하나씩 넣어보는데 그 개수는 실제 자동차의 개수보다 작아야 한다.
(37) : 첫 번째와 두 번째에서 렌탈한 총 개수를 RENTAL_CREDIT(=10)과 곱하여 reward에 저장한다
(38~39) : num_of_cars_(n)_loc에 렌탈한 자동차 개수를 각각 빼고 저장한다

def figure_4_2(constant_returned_cars=True):
    value = np.zeros((MAX_CARS + 1, MAX_CARS + 1))
    policy = np.zeros(value.shape, dtype=np.int)

    iterations = 0
    _, axes = plt.subplots(2, 3, figsize=(40, 20))
    plt.subplots_adjust(wspace=0.1, hspace=0.2)
    axes = axes.flatten()
    while True:
        fig = sns.heatmap(np.flipud(policy), cmap="YlGnBu", ax=axes[iterations])
        fig.set_ylabel('# cars at first location', fontsize=30)
        fig.set_yticks(list(reversed(range(MAX_CARS + 1))))
        fig.set_xlabel('# cars at second location', fontsize=30)
        fig.set_title('policy {}'.format(iterations), fontsize=30)

        # policy evaluation (in-place)
        while True:
            old_value = value.copy()
            for i in range(MAX_CARS + 1):
                for j in range(MAX_CARS + 1):
                    new_state_value = expected_return([i, j], policy[i, j], value, constant_returned_cars)
                    value[i, j] = new_state_value
            max_value_change = abs(old_value - value).max()
            print('max value change {}'.format(max_value_change))
            if max_value_change < 1e-4:
                break

        # policy improvement
        policy_stable = True
        for i in range(MAX_CARS + 1):
            for j in range(MAX_CARS + 1):
                old_action = policy[i, j]
                action_returns = []
                for action in actions:
                    if (0 <= action <= i) or (-j <= action <= 0):
                        action_returns.append(expected_return([i, j], action, value, constant_returned_cars))
                    else:
                        action_returns.append(-np.inf)
                new_action = actions[np.argmax(action_returns)]
                policy[i, j] = new_action
                if policy_stable and old_action != new_action:
                    policy_stable = False
        print('policy stable {}'.format(policy_stable))

        if policy_stable:
            fig = sns.heatmap(np.flipud(value), cmap="YlGnBu", ax=axes[-1])
            fig.set_ylabel('# cars at first location', fontsize=30)
            fig.set_yticks(list(reversed(range(MAX_CARS + 1))))
            fig.set_xlabel('# cars at second location', fontsize=30)
            fig.set_title('optimal value', fontsize=30)
            break

        iterations += 1

    plt.savefig('../images/figure_4_2.png')
    plt.close()

(2) : value : [(0~21), (0~21)]의 범위를 갖고 첫 번째와 두 번째 지점이 각 개수의 자동차를 갖는 모든 경우의 수를 나타낸다. 각 위치의 가치를 저장하기 위한 table이다
(3) : policy : 각 모든 경우의 수에서 정책을 저장할 table이다.
(5) : interation 반복회수를 저장하기 위한 변수
(18) : policy evaluation을 위한 반복문을 시작한다
(19) : 기존의 value를 old_value 변수에 deepcopy한다.
(20~21) : 모든 경우의 수에 대해 반복한다

`figure 4.3`

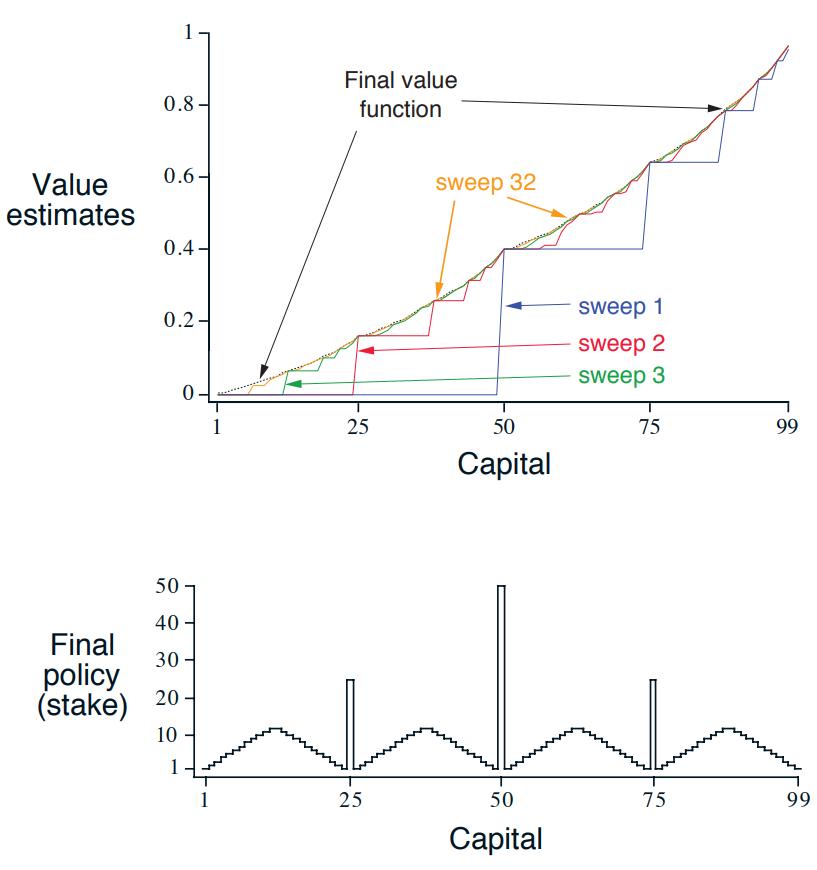
figure_4_3

도박사의 문제

연속된 동전 던지기의 결과를 맞추는 내기를 한다.

앞면 : 내건 액수만큼 돈을 딴다.
뒷면 : 내건 액수만큼 돈을 잃는다.
목표금액 100달러를 따거나 돈을 모두 잃으면 게임은 끝난다.

매번의 동전 던지기에서, 내걸 액수를 정해야 한다. 금액의 단위는 1달러다. 이 문제를 할인되지 않은 에피소딕 유한 MDP로 형식화할 수 있다. 상태는 보유한 자금의 액수 $s \in {1, 2, …, 99}$이고 행동은 내기에 거는 돈의 액수 $a \in { 0, 1, … \min(s, 100-s)}$이다. 도박사가 자신의 목표에 도달하게끔 하는 행동에 대한 보상은 +1이고 이를 제외한 나머지 행동의 보상은 0이다. 이제 상태 가치 함수로부터 각 상태에서 도박사가 돈을 딸 확률을 계산할 수 있다. 이 예제에서 어떤 정책이란 도박사가 보유한 자금의 액수와 도박사가 내거는 돈의 액수 사이의 관계를 규정하는 것이다. 최적 정책은 도박사가 목표에 도달할 확률을 최대로 만든다. 동전의 앞면이 나올 확률을 $p_h$라고 할 때, $p_h$를 알고 있다면, 문제 전체를 알고 있는 것이며, 예를 들면 가치 반복을 통해 이 문제를 풀 수 있다. figure 4.3은 가치 반복의 연속된 일괄 계산 과정에서 가치 함수가 변화하는 것과 $p_h=0.4$인 경우에 대해 가치 반복이 도달한 최종 정책을 보여준다. 이 정책은 최적 정책이지만 유일한 최적 정책은 아니다. 사실, 최적 가치 함수 측면에서 $\text{argmax}$의 최대화 조건을 만족하는 여러 행동이 있고, 각 행동에 상응하는 최적 정책을 모아놓은 집합이 있다.

# goal
GOAL = 100
# all states, including state 0 and state 100
STATES = np.arange(GOAL + 1)
# probability of head
HEAD_PROB = 0.4

def figure_4_3():
    # state value
    state_value = np.zeros(GOAL + 1)
    state_value[GOAL] = 1.0

    sweeps_history = []

    # value iteration
    while True:
        old_state_value = state_value.copy()
        sweeps_history.append(old_state_value)

        for state in STATES[1:GOAL]:
            # get possilbe actions for current state
            actions = np.arange(min(state, GOAL - state) + 1)
            action_returns = []
            for action in actions:
                action_returns.append(
                    HEAD_PROB * state_value[state + action] + (1 - HEAD_PROB) * state_value[state - action])
            new_value = np.max(action_returns)
            state_value[state] = new_value
        delta = abs(state_value - old_state_value).max()
        if delta < 1e-9:
            sweeps_history.append(state_value)
            break

    # compute the optimal policy
    policy = np.zeros(GOAL + 1)
    for state in STATES[1:GOAL]:
        actions = np.arange(min(state, GOAL - state) + 1)
        action_returns = []
        for action in actions:
            action_returns.append(
                HEAD_PROB * state_value[state + action] + (1 - HEAD_PROB) * state_value[state - action])

        # round to resemble the figure in the book, see
        # https://github.com/ShangtongZhang/reinforcement-learning-an-introduction/issues/83
        policy[state] = actions[np.argmax(np.round(action_returns[1:], 5)) + 1]

    plt.figure(figsize=(10, 20))

    plt.subplot(2, 1, 1)
    for sweep, state_value in enumerate(sweeps_history):
        plt.plot(state_value, label='sweep {}'.format(sweep))
    plt.xlabel('Capital')
    plt.ylabel('Value estimates')
    plt.legend(loc='best')

    plt.subplot(2, 1, 2)
    plt.scatter(STATES, policy)
    plt.xlabel('Capital')
    plt.ylabel('Final policy (stake)')

    plt.savefig('../images/figure_4_3.png')
    plt.close()

(2) : 목표 금액인 100을 정의한다
(4) : 모든 가능한 상태 [0~100] 숫자열을 얻는다.
(6) : 앞면이 나올 확률인 0.4를 정의한다.
(9~11) : [0~100]의 범위에서 GOAL인 100만 1의 값을 가지는 상태가치 배열 state_value를 정의한다.
(13) : // 각 iteration에서의 state_value를 기록하기 위한 배열 sweeps_history를 초기화한다
(17) : state_value 배열을 업데이트하기 위해 기존의 값들을 old_state_value에 깊은 복사한다
(18) : 위에서 옮겨둔 old_state_value를 sweeps_history에 축한다.
(20) : 종료상태(0, 100)를 제외한 모든 상태에 대해서 반복을 수행한다(=[1~99])
(21) : actions에 모든 가능한 action 의 배열을 저장한다.

Park Wooseong

단단한 강화학습 코드 정리, chap4

`figure 4.2`

`Car Rental`

`figure 4.3`

참고

torch 시행착오/패턴

JAX 시행착오/패턴

파이썬 헷갈리는 것 정리

JAX 라이브러리 공부 메모