머신러닝 회귀 성능지표 machine leanring regression metrix
노름
일반적으로 원소가 $n$개인 벡터 v의 노름은
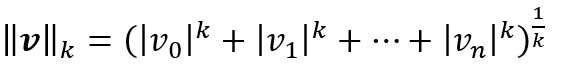
으로 정의한다.
- $l_{0}$은 벡터에 있는 0이 아닌 원소의 개수이며, $l_{\infty}$은 벡터에서 가장 큰 절댓값이 된다.
- 노름의 지수가 클 수록 큰 값의 원소에 치우치며 작은 값은 무시한다. 그래서 RMSE가 MAE보다 더 이상치에 민감하다. 하지만 (종 모양 분포의 양 끝단처럼) 이상치가 매우 드물면 RMSE가 잘 맞아 일반적으로 널리 사용된다.
평균제곱오차(RMSE)
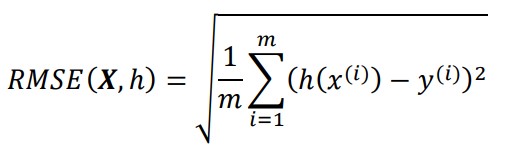
| 유클리디안 노름에 해당한다. $l_{2}$ 노름이라고도 부르며 $ | \cdot | _{2}$ 또는 $ | \cdot | $ 로 표시한다. |
평균절대오차(MAE) = 평균 절대 편차
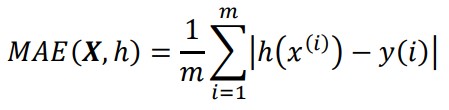
맨해튼 노름이라고도 하며 $l_{1}$ 노름에 해당한다.
RMSE와 MAE 모두 예측값의 벡터와 타깃값의 벡터 사이의 거리를 재는 방법이다.
결정 계수($R^{2}$)
결정계수(coefficient of determination): 모델 성능을 잘 해석하기 위해 만든 $MSE$의 표준화된 버전, 타깃의 분산에서 모델이 잡아낸 비율
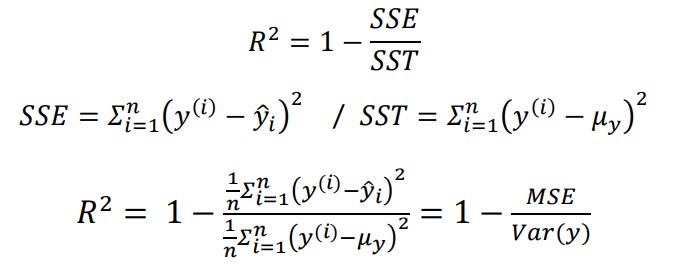
ex)
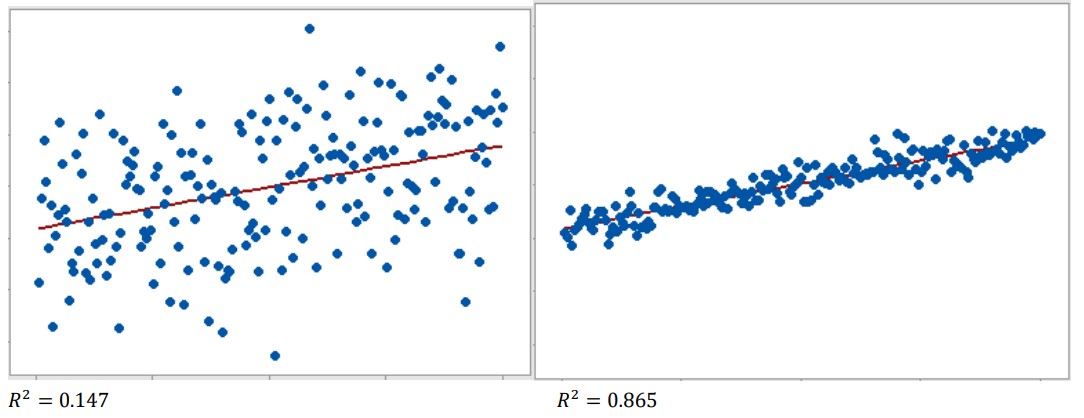
$R^{2}$이 높다 = 분산의 설명력이 높다.
조정된 결정 계수(adjusted $R^{2}$)
다중회귀분석의 경우 설명 변수를 계속 더하게 된다면 잔차항의 제곱합 $R^{2}$값이 높아지게 된다. 이런 경우 단순히 $R^2$를 증가시키기 위해 종속변수의 설명에 중요하지 않은 독립변수를 추가 시키는 경우가 발생할 수 있는데, 이런 단점을 보완하기 위해 조정된 결정 계수가 필요하다.
$R_{adj}^{2} = 1-\frac{(1-R^{2})(n-1)}{n-p-1}=1-(\frac{n-1}{n-p-1}\times\frac{SSE}{SST})$
- $n$ : 표본의 수
- $p$ : 설명 변수의 개수
$p$가 높아질 수록 $R_{adj}^{2}$ 가 감소하게 되어 $p$를 높이면 $R^{2}$가 높아지는 현상을 상쇄하게 된다
출처
- Aurelien, Geron, 『핸즈온 머신러닝』, 박해선, 한빛미디어(2020)