머신러닝 분류 성능지표 machine learning classification metrix
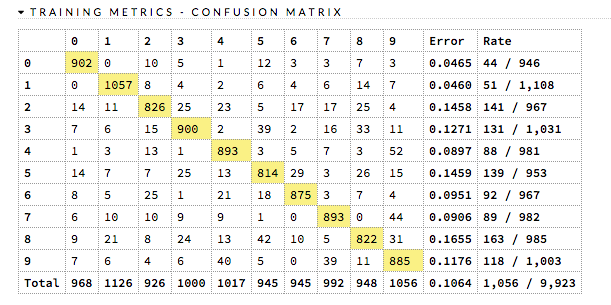
오차 행렬

- 정밀도(precision) = $\frac{TP}{TP+FP}$
True로 분류된 것 중에 실제로True인 비율
- 진짜 양성 비율(TPR) = 재현율(recall) = $\frac{TP}{TP+FN}$
- 실제
True중에True로 분류된 비율
- 실제
- 거짓 양성 비율(FPR) = $\frac{FP}{FP+TN}$
- 실제
False중에True로 분류된 비율
- 실제
- 진짜 음성 비율(TNR) = 특이도(specificity) = $\frac{TN}{FP+TN}$
- 실제
False중에False로 분류된 비율
- 실제
$FPR=\frac{FP}{FP+TN}=1-TNR=1-\frac{TN}{FP+TN}$
ex)
f1 score
정밀도(precision)와 재현율(recall)의 조화평균
상황에 따라 정밀도, 재현율의 중요도가 다를 수 있다.
ex)
- 어린이를 위한 음란물 필터 (좋은 것:
True) : 좋은 것이 몇개 걸러지더라도(낮은 재현율) 안전한 것들만 노출시키는(높은 정밀도) 분류기를 선호할 것이다. - 도둑을 잡아내는 감시 카메라 (도둑 :
True): 도둑이 아닌 사람을 도둑으로 감지하더라도(낮은 정밀도) 실제 도둑을 잡을 확률을 높이는(높은 재현율) 알고리즘을 선호할 것이다.
f beta score
$F$ 점수의 일반화된 조화 평균 식
$\beta$가 1보다 크면 재현율이 강조되고 1보다 작으면 정밀도가 강조된다
$\beta$가 1일때의 점수를 $F_{1}$ 점수라고 한다.
$\beta$의 값으로써 두 가지가 가장 많이 사용된다
- $\beta=2$ : 재현율의 비중이 정밀도보다 높을 때
- $\beta=0.5$ : 재현율의 비중이 정밀도보다 낮을 때
$F_{\beta}$ score에서 $\beta$가 아니라 $\beta^{2}인 이유$
PR Curve
다른 임계값에 대한 정밀도와 재현율간의 트레이드 오프를 보여준다.
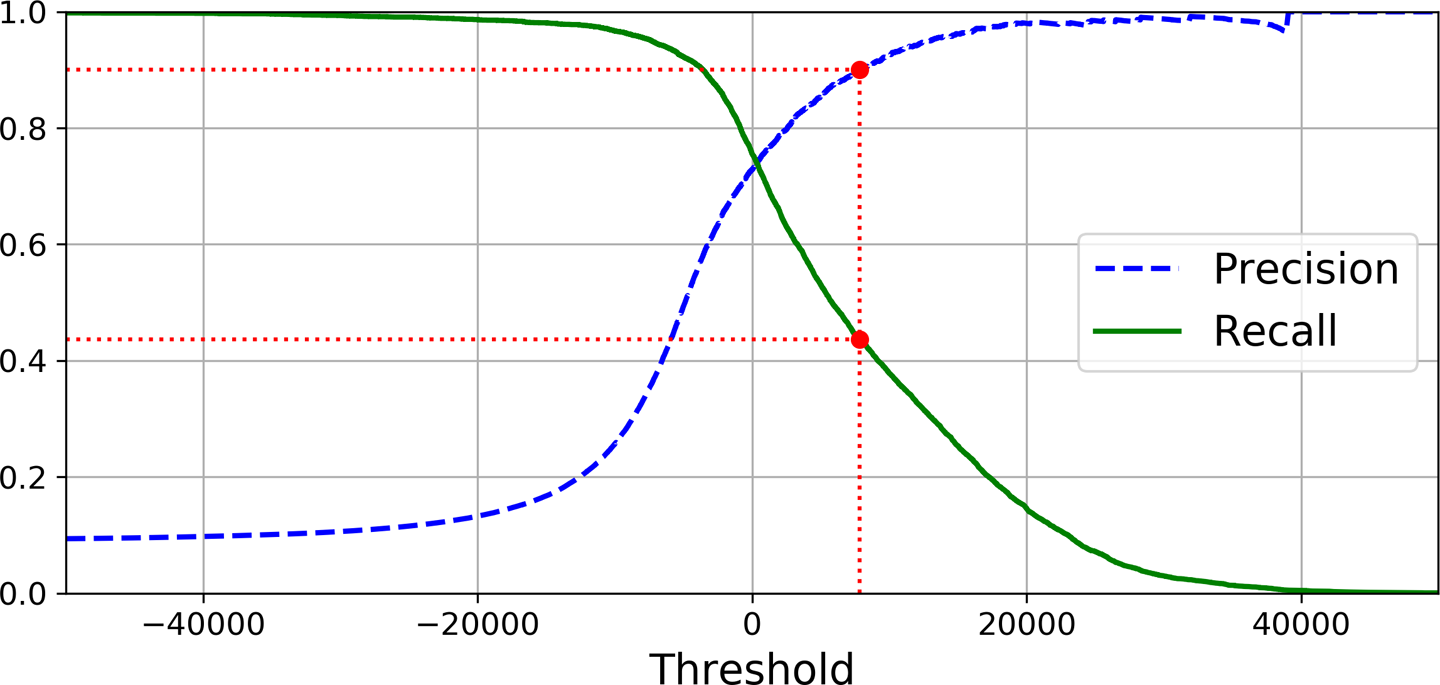
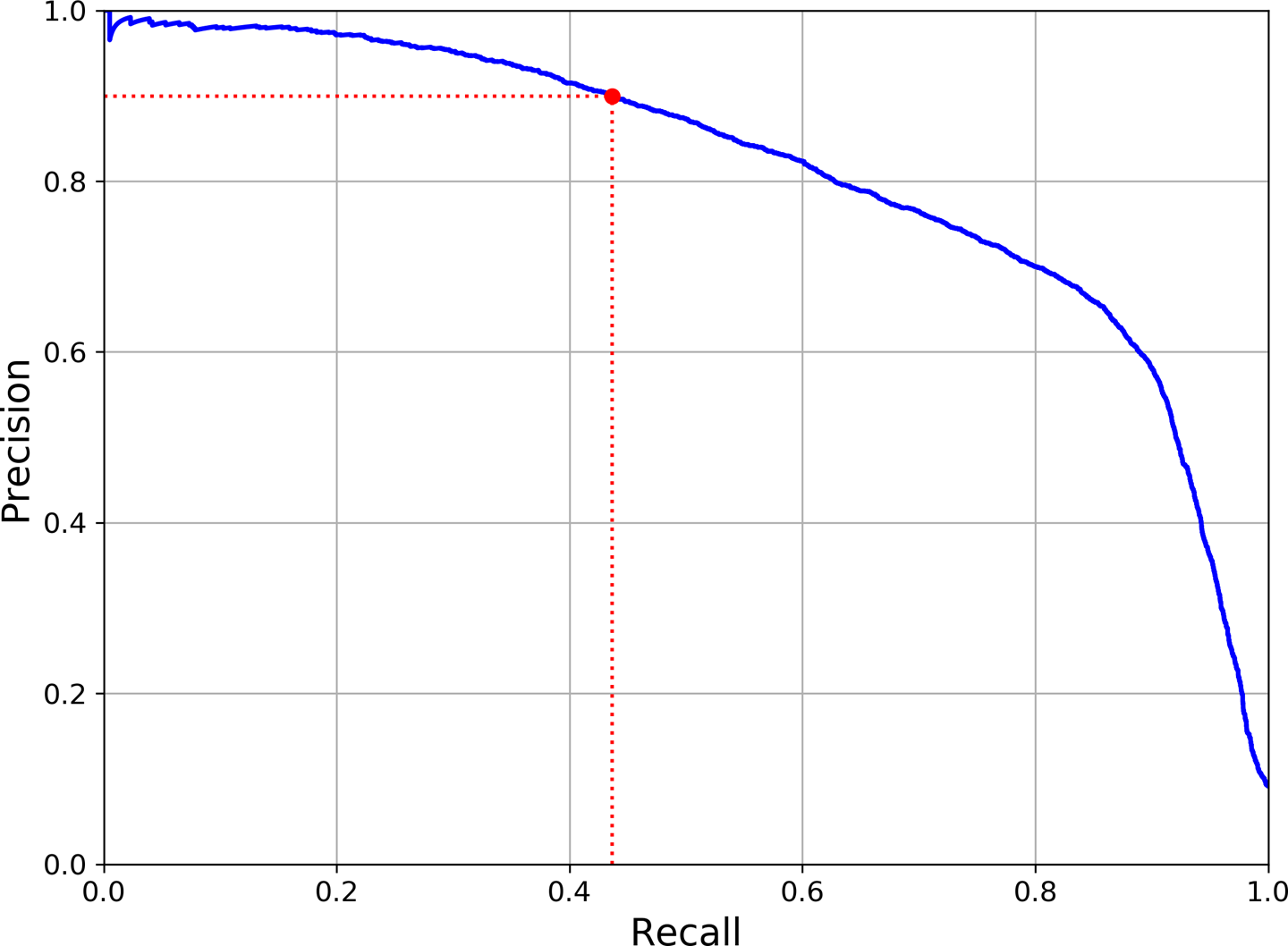
위 사진의 경우 재현율 80% 근처에서 정밀도가 급격하게 줄어드는데 이 하강점 지점을 정밀도/재현율 트레이드오프로 선택하는 것이 좋다.
정밀도 곡선이 재현율 곡선에 비해 왜 더 울퉁불퉁할까. 그것은 임곗값을 올리더라도 정밀도가 가끔 낮아질 때가 있기 때문이다. 일반적으로는 더 높아져야 한다. 그 이유는 아래 사진을 보면 알 수 있다.
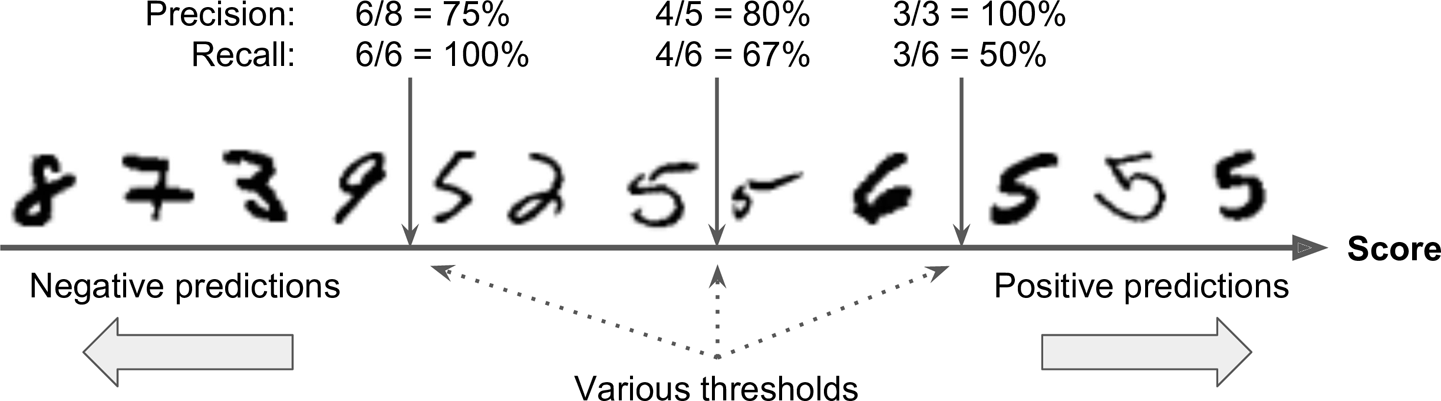 가운데 임곗값에서 오른쪽으로 숫자 하나만큼 이동하면 정밀도는 80%에서 75%로 줄어든다. 반면 재현율은 임곗값이 올라감에 따라 줄어들 수 밖에 없어 부드러운 곡선이다.
가운데 임곗값에서 오른쪽으로 숫자 하나만큼 이동하면 정밀도는 80%에서 75%로 줄어든다. 반면 재현율은 임곗값이 올라감에 따라 줄어들 수 밖에 없어 부드러운 곡선이다.
다시 말하자면 Recall이 낮으면 True인 것에 대해서 True라고 판정하지 못한것이 많다는 뜻이고 Precision은 True라고 예측한 것중에 True인 것들인데 그에따라 범위를 좁히면서 적은것들(난이도 쉬운 것들)에 대해 잘 맞추기에 수치가 높은 것이다. 그러면 True라고 예측한 것들의 분모가 줄어드는데 거기서 하나라도 False인 것이 나온다면 변동이 크기 때문에 Preicison이 커지는 부분에서 Precision 그래프가 튀는 것이다.
ROC Curve
- 진짜 양성 비율(TPR) = 재현율(recall) = $\frac{TP}{TP+FN}$
- 실제 True중에 True로 분류된 비율
- 거짓 양성 비율(FPR) = $\frac{FP}{FP+TN}$
- 실제 False중에 True로 분류된 비율
이진 분류에서 널리 사용한다. 거짓 양성 비율(FPR)에 대한 진짜 양성 비율(TPR, Recall)의 비율, True로 분류된 것들 중에서 실제 값이 어떤것이었느냐에 대한 트레이드오프를 나타낸다.
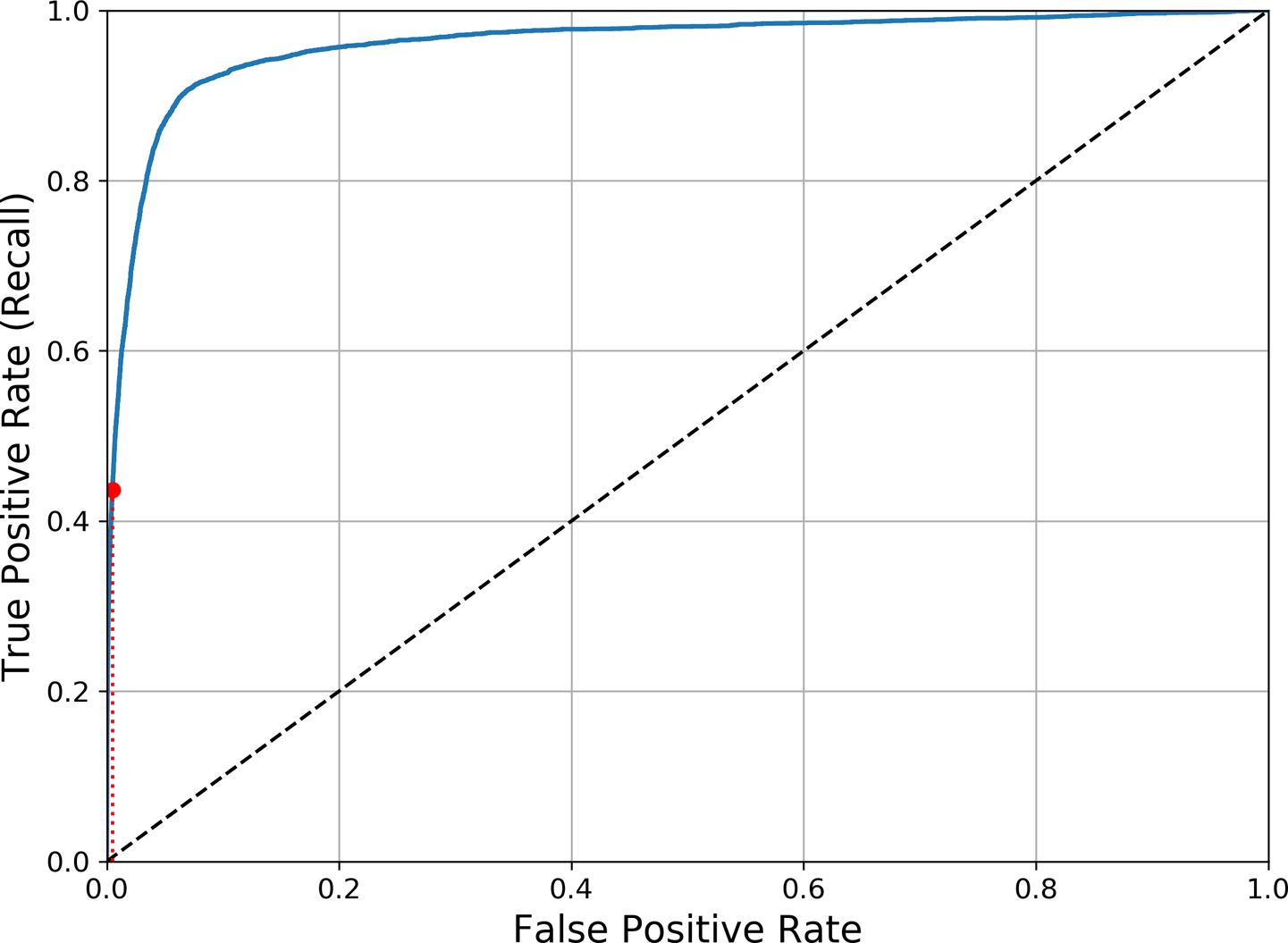
재현율(TPR)이 높을수록 많은 것을 True로 분류하게 된다는 뜻인데 그것으로 인해 거짓 양성(FPR)이 늘어난다. 점선은 완전 랜덤 분류기이며, 이와 멀수록(왼쪽 모서리에 가까울수록) 성능이 좋다는 뜻이다
AUC
곡선 아래의 면적(area under the curve) 완전한 분류기는 1에 가까울 수록 성능이 좋다는 뜻이며 완전 랜덤 분류기는 0.5이다.
PR curve vs ROC curve
PR curve는 양성 클래스가 드물거나 거짓 음성보다 거짓 양성이 더 중요할 때 그렇지 않으면 ROC curve를 사용한다.
- 정밀도(precision) = $\frac{TP}{TP+FP}$
- True로 분류된 것 중에 실제로 True인 비율
- 진짜 양성 비율(TPR) = 재현율(recall) = $\frac{TP}{TP+FN}$
- 실제 True중에 True로 분류된 비율
- 거짓 양성 비율(FPR) = $\frac{FP}{FP+TN}$
- 실제 False중에 True로 분류된 비율
예를들어 False가 훨씬 많다고 가정하자 그러면 FPR은 실제 음성인 것 중에 True로 예측된 것들인데, 이것은 분모가 매우 크고(실제 음성의 수) 분자가 작으므(실제로 적은데 예측치이므로 그 이하이다)로 낮게 나오고 또한 Recall은 적당히 타협해도 많은 True를 True로 분류할 수 있기 때문에 성능이 좋게 나오게 된다. 하지만 이경우 PR curve에서는 적당히 타협하느라 True로 분류해버린 False들이 들키게 되어 이럴 경우 PR이 좋은 것이다.
FFFFFFFFF~FFFFFFFFFF (1) FFFFFTF (2) FFFFTFTTTFTTTTT
- 쉽게 설명하면 ~부분이 정말 많다고 하자
- 그렇다면 (1)을 threshold로 하던 (2)로 하던 F의 비중이 매우 많기 때문에 FPR이 낮게 나올 것이다(실제
False가 분모이므로). - 그리고 많은 T의 대다수를 T로 분류할 수 있게 될 것이다(Recall 상승). 그래서 성능이 높아보이는 착각을 일으킬 것이다.
PR curve는Preicison에서True로 분류된 것(Threshold 우측)중에서 실제True를 검사하는데 여기서 (1)과 (2)사이에 있는 F들이 성능지표에 포함되기 때문에False가 훨씬 많은 경우 PR curve가 좋다.
출처
- Aurelien, Geron, 『핸즈온 머신러닝』, 박해선, 한빛미디어(2020)
- https://en.wikipedia.org/wiki/F-score
- https://developers.google.com/machine-learning/crash-course/classification/roc-and-auc?hl=ko
- https://docs.h2o.ai/h2o/latest-stable/h2o-docs/performance-and-prediction.html?_ga=2.174562212.72305442.1656698706-3838241.1656698706


