볼츠만 머신, Boltzmann machine

볼츠만 머신

1985년 제프리 힌튼과 테렌즈 세즈노스키가 발명했다.

완전 연결된 신경망이며 확률적(stochastic) 뉴런을 기반으로 한다. 계단 함수를 사용하여 결정론적으로 출력값을 만들지 않고 이 뉴런은 어느 정도 확률을 가지면 1을 출력하고 아니면 0을 출력한다. 이 인공 신경망에서 사용하는 확률 함수는 (통계 역학에서 사용하는) 볼츠만 분포에 기초하고 있기 때문에 여기에서 이름이 유래되었다.

[i번째 뉴런이 1을 출력할 확률]

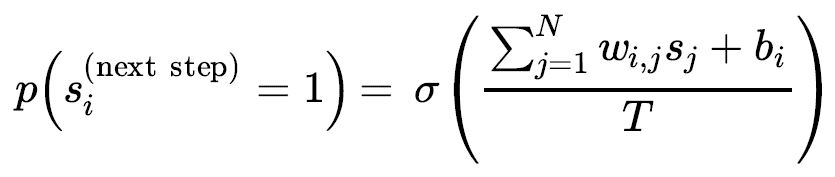
• $s_{j}$ : $j$번째 뉴런의 상태(0 또는 1)
• $w_{i,j}$ : $i$번째 뉴런과 $j$번째 뉴런 사이의 연결 가중치, $w_{i,i}=0$
• $b_{i}$ : $i$번째 뉴런의 편향. 이를 위해 네트워크에 편향 뉴런을 추가한다.
• $N$ : 네트워크에 있는 뉴런 수
• $T$ : 네트워크의 온도, 온도가 높으면 출력은 더욱 랜덤해진다.(확률이 50%에 가까워짐)
• $\sigma$ : 로지스틱 함수

볼츠만 머신의 뉴런은 가시 유닛(visible unit)과 은닉 유닛(hidden unit) 두 개의 그룹으로 나뉘어 있다. 모든 뉴런은 동일한 확률적 방식으로 작동한다. 하지만 가시 유닛에서만 입력을 받고 출력을 내보낸다.

확률적이기 때문에 볼츠만 머신은 고정된 설정으로 안정화되지 못하고 대신 여러 설정으로 계속 전환된다. 하지만 충분히 긴 시간동안 실행한다면 특정 설정이 관측될 확률은 원래 설정이 아니라 연결 가중치와 편향만의 함수가 될 것이다.(카드 묶음을 충분히 많이 섞으면 초기 상태와 상관없어지는 것과 비슷하다). 네트워크가 이 상태에 도달하면 원래 설정은 잊힌다. 이를 열평형(thermal equilibrium)이라고 한다.(설정은 계속해서 바뀌지만) 네트워크가 열평형에 도달하도록 적절하게 네트워크의 파라미터를 지정하고 상태를 관찰함으로써 다양한 종류의 확률 분포를 시뮬레이션 할 수 있다. 이를 생성 모델(generative model)이라고 한다.

볼츠만 머신을 훈련시킨다는 것은 훈련 세트의 확률 분포를 근사하는 네트워크의 파라미터를 찾는다는 뜻이다. 예를 들어 세 개의 가시 뉴런이 있고 훈련 세트가 (0, 1, 1) 쌍 75%, (0, 0, 1) 쌍 10%, (1, 1, 1) 쌍 15%로 이루어져 있다면 볼츠만 머신을 훈련시킨 후 거의 비슷한 확률 분포로 랜덤한 0, 1의 쌍을 생성할 수 있다. 예를 들면 75%의 확률로 (0, 1, 1) 쌍이 출력될 것이다.

이런 생성 모델은 여러 방면으로 사용될 수 있다. 예를 들어 이미지에 훈련시킨 후 불완전하고 잡음 섞인 이미지를 네트워크에 주입하면 자동으로 이미지를 적절히 복원할 것이다. 또한 생성모델을 분류 작업에 사용할 수도 있다. 훈련 이미지 클래스를 인코딩하는 몇 개의 가시 뉴런만 추가하면 된다. (에를 들면 10개의 가시 뉴런을 추가하고 훈련 이미지가 5일 때 다섯 번째 뉴런만 켠다). 그런 다음 새로운 이미지가 주어지면 해당하는 클래스를 나타내기 위해 네트워크는 자동으로 적절한 가시 뉴런을 켤 것이다.(즉, 이미지가 5라면 다섯 번째 가시 뉴런만 켜질 것이다.)

안타깝게도 볼츠만 머신을 훈련시키기 위한 효율적인 방법은 없다. 그러나 제한된 볼츠만 머신은 매우 효율적인 훈련 알고리즘이 개발되었다.

제한된 볼츠만 머신

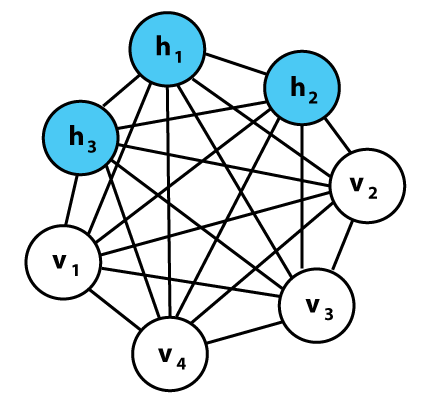
제한된 볼츠만 머신(restricted Boltzmann machine, RBM)은 가시 유닛과 히든 유닛 사이에만 연결이 있고 가시 유닛들 사이와 은닉 유닛들 사이에는 어떤 연결도 없는 볼츠만 머신이다.

3개의 가시 유닛과 4개의 히든 유닛을 가진 RBM

2005년에 미구엘 카레이라 페르미닝과 제프리 힌튼이 CD(Contrastive Divergence)라는 매우 효율적인 훈련 알고리즘을 소개했다.

작동원리

알고리즘이 가시 유닛의 상태를 $x_{1},x_2,…,x_n$으로 설정하는 식으로 훈련 샘플 $x$를 네트워크에 주입한다. 그런 다음

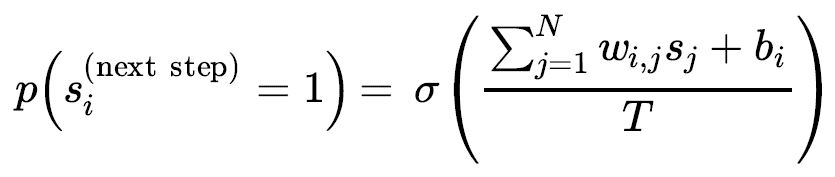
을 적용하여 은닉 유닛의 상태를 계산한다. 이렇게 하여 은닉 벡터 $h$를 얻는다. ($h_i$는 $i$번째 유닛의 상태). 그 다음에 같은 확률식을 적용하여 가시 유닛의 상태를 계산한다. 이렇게 하면 벡터 $x’$를 얻는다. 그리고 다시 한번 은닉 유닛의 상태를 계산하여 벡터 $h’$를 얻는다.

그런 다음 아래 규칙을 적용하여 각 연결 가중치를 업데이트한다.

[Contrastive divergence weight update]

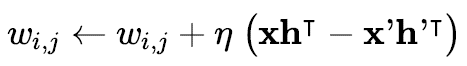
• $\eta$ : 학습률

이 알고리즘의 최대 장점은 네트워크가 열평형에 도달할 때까지 기다릴 필요가 없다. 이 네트워크는 정방향, 역방향, 그리고 다시 정방향으로 계산이 진행되는 것이 전부이다. 이는 이전 알고리즘에 비해 비교할 수 없을 정도로 매우 효율적이다. 이것이 다층 RBM에 기초한 딥러닝이 처음으로 성공하게 된 핵심 요소였다.

강화학습에서의 볼츠만 정책

ε-greedy 정책은 훈련이 진행됨에 따라 무작위로 행동을 선택할 확률 $\varepsilon$을 감소시킴으로써 탐험과 활용의 균형을 맞춘다. 이 정책의 한 가지 문제는 탐험 전략이 너무 단순하다는 점이다. 에이전트는 무작위로 탐험하고 이전에 학습한 환경에 대한 어떤 지식도 이용하지 않는다.

볼츠만 정책은 상대적인 $Q$ 가치를 이용하여 행동을 선택함으로써 무작위 탐험을 향상하고자 한다. 상태 $s$에서 $Q$가치를 최대화 하지 않지만 상대적으로 높은 $Q$ 가치를 갖는 다른 행동을 선택할 확률도 높을 것이다. 이렇게 하면 $Q$ 가치를 최대화하는 행동 선택에서 벗어나면서도 더 유망한 행동을 탐험하는 데 집중하는 효과를 갖는다.

볼츠만 정책을 생성하기 위해 softmax 함수를 적용함으로써 상태 $s$에서 모든 행동 $a$에 대한 $Q$ 가치의 확률분포를 만든다. 소프트맥스 함수에 온도(temperature) 파라미터 $\tau \in (0, \infty)$를 추가하여 확률 분포의 균일한 정도나 집중된 정도가 얼마인지를 조정할 수 있다.

• $\tau$ 값을 크게 하면 확률 분포는 더 균일해지고 (다 똑같이 작아지기 때문)
• $\tau$ 값을 작게 하면 확률 분포는 더 집중된 분포를 갖는다.

그런 다음 $(4.7)$에 표현된 분포에 따라 행동을 선택한다.

\[p_{\text{softmax}}(a \mid s)=\frac{e^{Q^{\pi}(s,a)}}{\sum_{a'}e^{Q_{\pi}(s,a')}} \tag{4.6}\] \[p_{\text{boltzmann}}(a \mid s)=\frac{e^{Q^{\pi}(s,a)/\tau}}{\sum_{a'}e^{Q_{\pi}(s,a')/\tau}} \tag{4.7}\]

볼츠만 정책에서 온도 파라미터 $\tau$의 역할은 ε-greedy 정책에서 ε의 역할과 유사하게 탐험을 권장한다.

	$x$	$p(x)$
$\text{boltzmann}, \tau=5$	$[1,2]$	$[0.45,0.55]$
$\text{boltzmann}, \tau=2$	$[1,2]$	$[0.38,0.62]$
$\text{softmax}$	$[1,2]$	$[0.27,0.73]$
$\text{boltzmann}, \tau=0.5$	$[1,2]$	$[0.12,0.88]$
$\text{boltzmann}, \tau=0.1$	$[1,2]$	$[0.00,1.00]$

훈련이 시작할 때 $\tau$ 값을 크게 하면 탐험을 권장하게 되고 시간이 지남에 따라 $\tau$가 감소하면서 정책이 탐욕적 정책에 가까워진다.

ε-greedy과 비교했을 때 볼츠만 정책의 주된 장점은 환경을 덜 무작위로 탐험ㅎ나다는 것이다. $\varepsilon$의 확률로 무작위 행동을 하는 대신, 에이전트가 $p_{\text{boltzmann}}(a \mid s)$의 확률로 행동을 선택하기 때문에 더 큰 값의 $Q$ 가치를 갖는 행동이 선택될 확률이 더 높다.(선택 확률이 1위 빼고 모두 같은 확률이 아니라 $Q$값의 순위와 같은 확률의 크기 순위를 갖는다.)

볼츠만 정책은 또한 ε-greedy 정책에 비해 $Q$ 가치 추정값과 행동 확률 사이의 관계를 더 부드럽게 만든다.

$\tau=1, \varepsilon=0.1$

$Q^{\pi}(s,a_1)$	$Q^{\pi}(s,a_2)$	$p_{\varepsilon}(a_1 \mid s)$	$p_{\varepsilon}(a_2 \mid s)$	$p_{B}(a_1 \mid s)$	$p_{B}(a_2 \mid s)$
1.00	9.00	0.05	0.95	0.00	1.00
4.00	6.00	0.05	0.95	0.12	0.88
4.90	5.10	0.05	0.95	0.45	0.55
5.05	4.95	0.95	0.05	0.53	0.48
7.00	3.00	0.95	0.05	0.98	0.02
8.00	2.00	0.95	0.05	1.00	0.00

위 결과와 같이 Boltzmann 정책은 ε-greedy에 비해 $Q$ 값의 상대적 관계를 고려하여 행동 확률 사이의 관계를 더 부드럽게 만드는 것을 볼 수 있다.

(의견) 강화학습에서 target으로 현재 step의 reward + 다음 step의 $Q$ 추저값으로 있을때가 많은데 이것은 지도학습에서의 label개념에 해당한다. 원래 딥러닝은 이 label이 고정되어 있다고 가정하지만 실제 강화학습에서는 target 또는 label이 바뀔 수 있다. 그런데 강화학습은 이것이 고정되어 있지 않아 학습이 불안정하여 수렴에 어렵다고 하는데 Boltzmann 정책이 이것을 약간 완화시켜줄 수 있지 않을까

그럼 무조건 Boltzmann 정책이 좋은 것일까??

아니다 일부 상태 공간에 대해 $Q$ 가치 추정값이 부정확할 때 볼츠만 정책을 사용하면 에이전트는 지역적 최솟값(local minimum)에 빠질 수 있다. 다음 예를 보자

$Q^{\ast}(s,a_1)=2,Q^{\ast}(s,a_2)=10$이라 하고 현재 추정값이 $\hat{Q^{\pi}}(s,a_1)=2.5,\hat{Q^{\pi}}(s,a_2)=-3$이라고 하자 이러면 $\tau=1$일 경우 $p(x)=[0.9959…, 0.0040…]$이다. 이러면 $a_2$를 탐험할 확률은 거의 사라질 것이다. 하지만 ε-greedy 정책은 $Q$ 가치 추정값에 관계없이 $p=\varepsilon/2$의 확률로 $a_2$를 선택한다. 이러면 시간이 지남에 따라 $Q$ 가치 추정값이 보정될 가능성이 높다.

물론 해결방법이 아예 없는 것은 아니다. 훈련 초기에 $\tau$값을 키워서 행동 확률 분포가 더 균일하게 만들고 $\tau$값을 점점 줄이면서 에이전트가 학습한 지식을 활용하도록 할 수 있다. $\tau$를 너무 빨리 감소시키면 정책이 지역 최솟값에 빠져버릴 수 있다.

출처

• Aurelien, Geron,『핸즈온 머신러닝』, 박해선, 한빛미디어(2020)
• https://en.wikipedia.org/wiki/Boltzmann_machine
• https://en.wikipedia.org/wiki/Restricted_Boltzmann_machine
• Laura Graesser, Wah Loon Keng,『단단한 심층 강화학습』, 김성우, 제이펍(2022)