알고리즘 PS 오답노트/팁
뒷 내용(21~40)은 “알고리즘 PS 오답노트/팁 2”에서 찾아볼 수 있다.
1.
dfs로 재귀적 탐색을 한다면 주어진 조건을 충족시키지 못한다는 것이 명백하거나, 주어진 조건을 충족했다면 함수를 종료해야한다.
BOJ 1941 문제에서 학생 수가 7명이 되면 탐색을 끝내야 하는데 학생수 7명을 체크하고 숫자를 하나 늘린다음에 함수를 끝내지 않아 8, 9, 10… 까지 계속 탐색하게 되어 시간초과가 일어났다.
함수를 종료시키는 방법으로는 if True ~ else: ~ 또는 if True return else: ~ 방법이 있을 수 있다.
2.
그래프 문제(ex. 다익스트라)를 풀 때 INF 설정에 주의해야 한다. BOJ 9370 문제에서 INF값으로 distance를 초기화하고 문제를 풀기 위해 distance를 도로의 길이의 최댓값인 1000에 1을 더해 1001로 했다. 이러면 안된다. 어떤 두 점 사이의 최대 길이는 (노드의 개수-1) X (도로의 최대 길이)가 되어야 한다. 순간 접한 두 점사이의 거리의 최댓값과 임의의 두 점 사이의 거리를 헷갈렸다. 효율적이지는 않지만 헷갈린다면 sys.maxsize를 쓰도록 하자.
3. operator chaining
1
2
3
4
5
6
7
>>> one = [1]
>>> 1 in one != 2 in one
False
>>> (1 in one) != (2 in one)
True
>>> ((1 in one) != 2) in one
True
문제의 조건을 판단하는 문제에서 첫번째와 같이 작성하여 특정 조건에 진입하지 못하게 되었다. 내가 가진 의도는 두 번째 처럼 계산되는 것이었다.
연산자 우선순위 문제인가 생각이 들어서 두번째, 세번째처럼 작성하였으나 모두 True를 반환하였다. (3번째 것도 True in one이어서 True를 반환하여 의도와 맞지 않기는 하다.)
파이썬 공식 문서를 보자.

정리하면 다음과 같다
파이썬은 C와 달리 a < b < c 사용이 가능하다
비교연산은 chain될 수 있는데 예를 들어 x < y <= z는 x < y and y <= z의 의미를 갖는다. 이를 comparison chaining이라고 한다.
확장해서 a op1 b op2 c ... y opN z는 a op1 b and b op2 c and ... y opN z의 의미를 갖고 이는 한번만 계산된다. (a op1 b를 하고 a op2 c를 또하지 않는다는 이야기다)
문제로 돌아가보자 그럼 내 식이었던
1
1 in one != 2 in one
은
1
2
1 in one and one != 2 and 2 in one
# == (1 in one) and (one != 2) and (2 in one)
과 같은 의미가 된 것이고 2 in one == False이기 때문에 False를 반환한 것이다.
4. sort(key=??)
파이썬은 정렬시에 key에 함수를 인자로 줄 경우 조건 외 부분은 기존의 순서를 유지한다. 기본 정렬이 아닐 경우 주의해야 한다.
예를 보자
1
2
3
>>> test = [[2, 3], [2, 2], [3, 2], [3, 1]]
>>> sorted(test)
[[2, 2], [2, 3], [3, 1], [3, 2]]
key에 아무것도 설정하지 않으면 생각하는 기본 순서대로 우선순위를 왼쪽에서 오른쪽으로 가면서 정렬한다.
다음 예를 보자
1
2
3
>>> test = [[2, 3], [3, 2], [2, 2], [3, 1]]
>>> sorted(test, key=lambda x: x[1])
[[3, 1], [3, 2], [2, 2], [2, 3]]
두번째 원소를 기준으로 정렬했다. 그런데 [3, 2]와 [2, 2]는 뒤에서부터 정렬하면 [2, 2]가 앞으로 나와야할 것 같지만 key에 들어간 함수로 정렬할 때는 요소 외의 이외 부분은 신경도 쓰지 않고 기존의 순서 ([3, 2], [2, 2])를 유지한다.
만약 뒤에부터 정렬하고싶다면
1
2
3
>>> test = [[2, 3], [3, 2], [2, 2], [3, 1]]
>>> sorted(test, key=lambda x: x[::-1])
[[3, 1], [2, 2], [3, 2], [2, 3]]
처럼 쓰면 될 것이다.
5. Dynamic Programming
아주 간단한 문제이다. 문제가 DP로 풀린다는 느낌이 올 경우 재귀코드로 헷갈리게 생각하지말고 일단 수학적으로 점화식을 떠올린 후에 그것을 코드로 옮기자.
6. Traveling Sales Person
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import sys
input = sys.stdin.readline
n_city = int(input())
graph = [list(map(int, input().split())) for _ in range(n_city)]
INF = int(1e9)
board = [[0] * (1 << n_city) for _ in range(n_city)]
def tsp(now, visited):
if visited == (1 << n_city) - 1:
if graph[now][0]:
return graph[now][0]
else:
return INF
if board[now][visited]:
return board[now][visited]
n_min = INF
for next in range(1, n_city):
if not graph[now][next]:
continue
if visited & (1 << next):
continue
n_min = min(n_min, graph[now][next]
+ tsp(next, visited | 1 << next))
board[now][visited] = n_min
return board[now][visited]
print(tsp(0, 1))
TSP 문제에서 모두 방문한 경우 마지막에 now에서 0으로가는 길을 설정할 때 길이 0이면 INF를 리턴해야 한다. 그래야 그것을 받은 호출자에서 그것을 최단경로로 선택하지 않는다. 나는 그러지 않고 그냥 반환했다가 길이 없음을 의미하는 0을 0으로 반환해서 그것이 선택되게 해서 틀렸다.
또 초기 board를 INF보다는 0으로 초기화하는 것이 빠른 것 같다. 뒤에서 조건판단할때는 상관이 없다. 그런데 INF로 초기화하면 시간초과가 났다. 그래서 실험을 해보았다.
7. index의 base 주의
가끔 코드의 직관성을 위해 index를 1부터 시작할 때가 있다. 예를 들어 도시의 이름이 1부터 N까지 주어지는 경우 같은 것이다. 그럴경우 각 요소의 속성을 배열에 저장할 경우 index 0부분에 어떤 수를 미리 집어넣고 append하는 경우가 있다. 그래프에서 간선의 목록을 표현할 때도 마찬가지이다. 하지만 파이썬은 기본적으로 zero-based이기 때문에 함수 사용시 주의해야 한다. 이로 인해 말도 안되는 실수가 나올 때가 있다.
예를 들어 1부터 8까지의 수 중에서 3개를 뽑는 조합을 구한다고 하자. 그럼 경우의 수는 $_8C_3$이 될 것이다. 그리고 해당 조합들을 구하려면 combinations(range(1, 8+1), 3)을 써야 한다. 하지만 나의 경우 실수로 combinations(range(8+1), 3)을 써서 한참 헤맸다. 요소가 1부터 시작하여 따로 장치를 해야 하는 경우 코드를 zero-based로 쓰지 않았는지 확인하자.
8.
이진트리의 순회는 dfs와 연관지어 생각하자. 중위 순회(preorder)는 root -> left -> right 순서로 방문하는데 이것은 dfs에서 children을 left -> right 순서로 탐색할 때 dfs의 탐색 순서와 같다.
또한 전위 순회(inorder)를 배열에 나열하게 되면 그 모습은 이진 트리를 1차원 선에 투영한 것과 같은 모양이다.
중위순회(preorder)은 tree의 root가 맨 앞에 있다.
9. 행렬에서 판단시 자주 쓰이는 연산
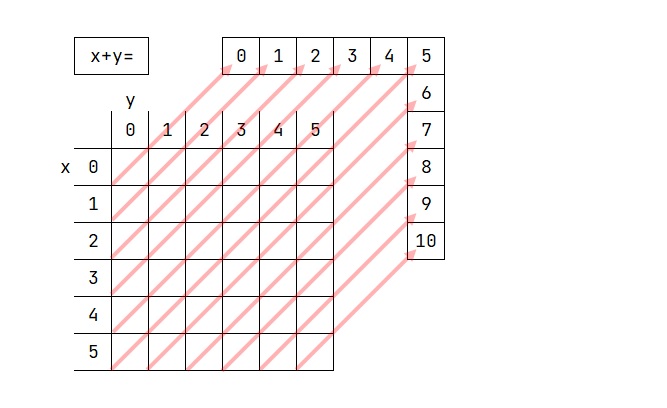
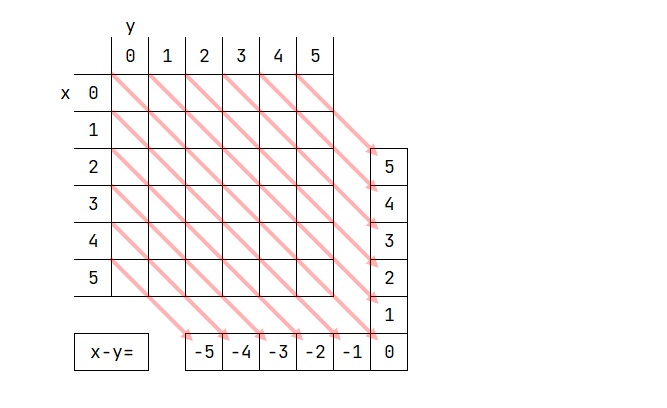
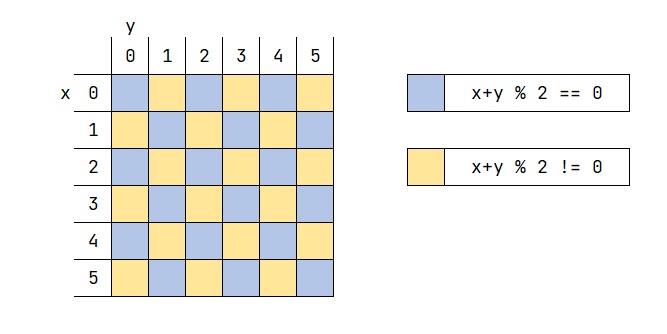
10.
AND를 반환해야 하는지 OR을 반환해야 하는지 답의 개수를 반환해야 하는지 가능여부를 반환해야 하는지를 판단하자.
1
2
if b or c or d:
return True
문제 형식이 위와 같이 or이 조건으로 사용되면 b, c, d 모두 판단하지말고 셋중하나라도 만족하면 바로 다음으로 넘어가야 한다.
파이썬에서 if 문을 쓸경우 최대한 빠르게 판단해준다.
1
2
3
4
5
6
7
8
9
10
11
12
>>> if (t := 4) > 3 or (t := 3) > 3 or (t := 2) > 3:
... pass
>>> print(t)
4
>>> if (t := 2) > 3 and (t := 3) > 3 and (t := 4) > 3:
... pass
>>> print(t)
2
비슷하게 개수를 찾는 문제와 가능 여부를 묻는 문제가 있다. LEETCODE 079 문제에서 가능 여부만 묻기 때문에 하위여러개 중 하나라도 만족하면 바로 True를 반환하면 된다. 근데 처음에 4개를 다 판단하고 리턴시에 or을 써서 시간초과가 났다. 문제의 조건을 잘 파악하고 필요없는 연산을 줄이자.
11.
구간합
- 값이 중간에 변경된다 : Segment Tree
- 값이 변경되지 않는다 : 누적합
12.
그래프 문제
- 다익스트라 : 기본적으로 사용, 한 지점에서 각 지점까지의 최소거리
- 벨만 포드 : 음수 간선이 있을때 최소거리 조회
- 플로이드 워셜 : 모든 지점에 대해 최소거리 조회
13.
MST, Undirected Graph
- 크루스칼: 간선이 Sparse
- Time complexity: $O(E\log{E})$
- 프림: 간선이 Dense
- Time complexity: $O(E\log{V})$
14.
XOR 연산은 결합법칙, 교환법칙이 성립한다.
XOR은 어떤 수에 대해 흔적을 놓거나 지우는 역할을 할 수 있다.
1
2
3
4
5
6
>>> 5 ^ 5
0
>>> 4 ^ 5 ^ 5
4
>>> 6 ^ 5 ^ 6
5
LEETCODE 136에서 배웠다. 어떤 배열에서 한 수를 제외하고 모두 두개씩 있다면 XOR연산을 누적하여 그 한 수를 구할 수 있다.
15. 그래프의 탐색 순서 전환
8번과 연관지어 생각하면 좋다.
- preorder(전위 순회) :
left->root->right - inorder(중위 순회) :
root->left->right - postorder(후위 순회) :
left->right->root
위 순회들을 순회 순서대로 한 배열에 저장했다고 하자
이때 left, root, right의 의미를 생각해보자 left, right는 subtree를 의미하며 root는 단일 노드다. 전위 순회의 가장 큰 특징은 root가 가운데 있으며 이 root의 인덱스를 통해 왼쪽과 오른쪽을 유일한 경우의 수로 나눌 수 있다. inorder, postorder의 경우에는 각각 left, right가 가운데에서 양쪽을 나누고 있긴 하지만 각각 범위를 모르기 때문에 유일한 경우로 나눌 수 없다.
그럼 preorder가 주어졌을 경우 이 것을 잘 활용해야 한다. 어떤 tree(subtree)가 있다고 했을 때 inorder이 주어졌을 경우 root가 맨 앞에 있다. postorder이 주어졌을 경우 root가 맨 뒤에 있다. 이 root의 인덱스를 주어진 preorder 배열을 통해 인덱스를 구하면 해당 tree의 left, right의 범위를 구할 수 있고 범위를 알 수 있다는 것은 노드 개수를 알 수 있다는 뜻이기도 하다.
이제 그 개수나 범위를 이용하여 inorder이나 postorder의 left, right를 구할 수 있고 이제 그것을 이용하여 재귀탐색을 할 수 있게 된다.
16. 1차원에 배치된 것들 사이의 거리
1차원에 배치된 것들 사이의 거리는 그 사이에 있는 요소들 사이의 거리의 합으로 나타낼 수 있다. 직접적으로 개념이 쓰이는 문제도 있지만 요소간의 거리를 1차원으로 만들어버릴 수 있는 문제도 있다.
예를 들어
a <-1-> b <-2-> c <-9-> d 로 배치되어 있다면 a-d의 거리는 (a<->b) + (b<->c) + (c<->d)와 같다. 당연한 말 같지만 문제를 풀 때 거리를 나타낼 때 쓰일 수 있다. 특히 크루스칼 알고리즘은 a<->b, b<->c를 union할 경우 a와 c의 조상이 같아지기 때문에 a<->c연산이 필요없다. 이렇게 크루스칼 알고리즘과 함께 자주 쓰이는 것 같다.
응용 문제
17. Union-Find 에서 조상을 찾을때는 parent 참조가 아니라 find를 쓰자
어떤 노드의 조상을 알고 싶다면 find_parent를 써야지 parent를 바로 참조하면 안된다.
다음 코드를 보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
NODE = 4
parent = [i for i in range(NODE+1)]
def find_parent(parent, x):
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a > b:
parent[a] = b
else:
parent[b] = a
edges = [(1, 2), (3, 4), (2, 3)]
for a, b in edges:
if find_parent(parent, a) != find_parent(parent, b):
union_parent(parent, a, b)
print(parent)
>>> [0, 1, 1, 1, 3]
4개의 노드가 있고 edges 의 순서대로 union을 하는 코드이다.
위 코드는 4개의 노드를 1-2, 3-4, 2-3 순서로 이은 후 parent를 출력한 것이다.
4번 노드의 parent는 1이지만 parent 리스트에는 3으로 저장되어있다.
아직 4번노드를 거치지 않았기 때문에 find_parent로 인해 parent가 업데이트되지 않은 것이다. 그러므로 어떤 노드의 parent를 알고 싶다면 find_parent 함수를 써야 한다.
또한 find_parent는 조상을 찾아가면서 parent를 업데이트하기 때문에 find_parent(parent, 4)를 호출한 후에는 parent[4] == 1이 될 것이다.
18. 그래프 탐색 시 그래프의 모든 정점이 연결되어 있지 않을 수도 있다.
BOJ 1707 문제에서 BFS로 알맞게 탐색하였으나 모든 정점이 연결되어 있다고 가정하여 시작점을 1로 놓았더니 틀렸다. 예를 들어 1, 2-3-4로 연결되어 있다면 2-3-4에 대한 탐색을 할 수 없게되기 때문이다. 이런 경우도 고려하여 모든 정점에 대해 탐색할 수 있게 해야 한다.
19. Union Find 연산에서 조상의 기준은 다르게 설정될 수 있다.
BOJ 16562 문제에서 Union-Find 알고리즘을 사용해야 한다는 것을 눈치챘다.
Union-Find (혹은 크루스칼) 알고리즘을 사용하면서 여태까지 인덱스로만 parent의 기준을 결정해서 습관적으로 parent를 인덱스(가 낮은 기준으)로 설정하였다. 하지만 일정한 기준만 있다면 조상의 기준을 인덱스로 하지 않아도 된다. 예를 들어 위 문제에서는 그래프로 연결된 집단 내에서 가장 친구비가 낮은 친구의 친구비만 취하면 된다. 그러므로 조상의 기준을 친구비로 한다면 어떤 집단의 조상은 친구비가 가장 낮은 친구가 된다. 그럼 그 값을 취하면 된다.
20. if문의 우선순위에 조심하자.
BOJ 1700 문제에서 if문의 우선순위를 놓쳐서 고생했다. 리스트에 같은 것이 있으면 안좋다는 전제 하에서, 반복문은 두 가지 조건에서 continue를 한다. value가 리스트에 있을 때, 또는 리스트의 길이가 N보다 작을 때이다. 그렇다면
value가 리스트에 있으면continue- 리스트의 길이가
N보다 작다면continue
둘 중 어느 것이 먼저 수행되어야 할까
1번이다. 만약 2번이 먼저 있다면 N이 3이고 1이 연속으로 두번 들어올때, 두번 다 리스트의 길이가 N보다 작으므로 리스트에 1을 두 번 넣게 된다. 문제상 리스트에 같은 것이 들어있으면 안좋기 때문에 이렇게 풀이를 설계하면 안된다.